In part one of our Math Heuristics series, we gave an overview of the 12 heuristics in Singapore Primary Math syllabus, with tips from the curriculum team at Seriously Addictive Mathematics (S.A.M) on how to solve various math word problems using them.
To recap, heuristics are strategies students can use to solve complex math word problems. They are general guidelines of what students can do to tackle a word problem when the solution is not obvious.

Besides using heuristics to solve a word problem, Singapore Math also adopts Polya’s 4-step problem-solving process:
- Understand the problem: What to find? What is known and unknown?
- Devise a plan: Choose the most suitable heuristic
- Carry out the plan: Solve the problem
- Look back: Check the answer
To solve word problems efficiently, students must be familiar with both the problem solving strategies (heuristics) and the problem solving process (Polya’s 4-step).
In this article, we will focus on 3 heuristics – Act it out, Draw a diagram/model, and Look for pattern(s).
Sample word problems are solved using these 3 heuristics and Poly’s 4-step process in a step-by-step worked solution provided by the curriculum team at S.A.M.
Heuristic: Act it out
Word Problem (Primary 2):
Ben cuts a cake into 5 equal pieces. He wants to eat some of the pieces of cake so that the fraction of cake he eats is smaller than the fraction of the cake left. What is the greatest possible fraction of the cake that Ben can eat?

Solution:
1. Understand:
What to find: The greatest possible fraction of the cake that Ben can eat.
What is known: The cake is cut into 5 equal pieces. The fraction of cake he eats is smaller than the fraction of the cake left.
2. Choose: Act it out
3. Solve:
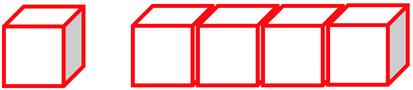
If Ben eats 1 piece, 4 pieces are left. 1⁄5 is smaller than 4⁄5
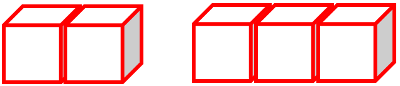
If Ben eats 2 pieces, 3 pieces are left. 2⁄5 is smaller than 3⁄5.

If Ben eats 3 pieces, 2 pieces are left. 3⁄5 is greater than 2⁄5. This does not match the word problem.
The greatest possible fraction of the cake that Ben can eat is 2⁄5.
4. Check:
Did I give the answer as a fraction? Yes
Is the fraction he ate smaller than the fraction left? Yes
Is it the greatest possible fraction of cake he can eat? Yes
Try solving the following word problem using Polya’s 4-step process.
Word Problem (Primary 1):
Alan, Ben and Carol are in the school’s Art Club. Their teacher, Mr Tan, wants two of them to join a contest. How many ways can Mr Tan choose two pupils?
Answer: Mr Tan can choose two pupils in 3 ways.
See the solution here.
Heuristic: Draw a diagram/model
Word Problem (Primary 2):
There were 158 children in a movie theatre. There were 267 more adults than children in the theatre. 236 of the adults were men. How many women were there in the theatre?
Solution:
1. Understand:
What to find: The number of women in the theatre.
What is known: There were 158 children. There were 267 more adults than children. There were 236 men.
2. Choose: Draw a diagram/model
3. Solve:
There were 158 children.

There were 267 more adults than children.
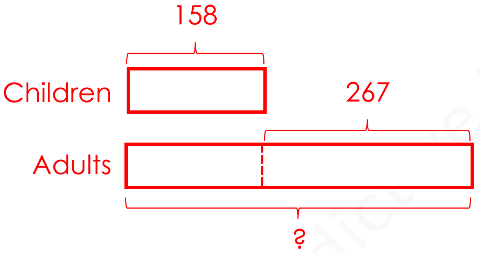
158 + 267 = 425
There were 425 adults in the theatre.
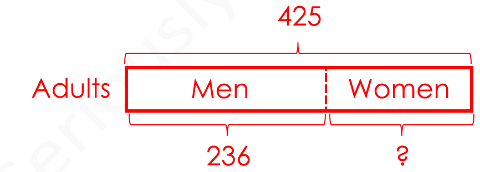
425 – 236 = 189
There were 189 women in the theatre.
4. Check:
How many adults were there? 236 + 189 = 425
Were there 267 more adults than children? 425 – 158 = 267. Yes
Try solving the following word problem using Polya’s 4-step process.
Word Problem (Primary 3):
The smaller of two numbers is 1217. The greater number is 859 more than the smaller number.
(a) What is the greater number?
(b) What is the sum of the numbers?
Answer:
(a) The greater number is 1217 + 859 = 2076.
(b) The sum of the numbers is 2076 + 1217 = 3293.
See the solution here.
Word Problem (Primary 5):
Tammy has 3 boxes of apples. Box A is 550 grams heavier than Box B and 770 grams heavier than Box C. The average mass of the 3 boxes is 2150 grams. Find the average mass of Box B and Box C. Give your answer in kilograms and grams.

Solution:
1. Understand:
What to find: The average mass of Box B and Box C.
What is known: Box A is 550 grams heavier than Box B. Box A is 770 grams heavier than Box C. The average mass of Box A, Box B and Box C is 2150 grams.
2. Choose: Draw a diagram/model
3. Solve:
Box A is 550 grams heavier than Box B.

Box A is 770 grams heavier than Box C.

2150 x 3 = 6450
The total mass of the 3 boxes is 6450 grams.
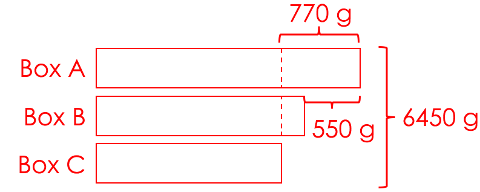
770 – 550 = 220
Box B is 220 grams heavier than Box C.
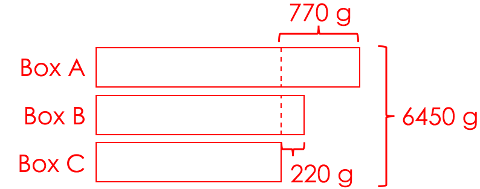
3 units = 6450 – 770 – 220 = 5460
1 unit = 5460 ÷ 3 = 1820
The mass of Box C is 1820 grams.
1820 + 220 = 2040
The mass of Box B is 2040 grams.
2040 + 1820 = 3860
The total mass of Box B and Box C is 3860 grams.
3860 ÷ 2 = 1930 grams
The average mass of Box B and Box C is 1 kilogram 930 grams.
4. Check:
What is the mass of Box A? 1820 + 770 = 2590 grams.
What is the total mass of the 3 boxes? 1820 + 2040 + 2590 = 6450.
Is the average mass of the 3 boxes 2150 grams? 6450 ÷ 3 = 2150 grams. Yes
Did I give the answer in kilograms and grams? Yes
Heuristic: Look for pattern(s)
Word Problem (Primary 4):
Carmen uses the letters in her name to form the pattern below.
C A R M E N C A R M E N C A …
What will be the 405th letter in the pattern?
Solution:
1. Understand:
What to find: The 405th letter in the pattern.
What is known: The pattern is form by the letters CARMEN. The pattern starts repeating itself from the 7th letter.
2. Choose: Look for patterns
3. Solve:
CARMEN is the repeating block of letters.
There are 6 letters in each block.
405 ÷ 6 = 67 remainder 3
There are 67 such blocks.
The remainder of 3 means we have to count 3 more letters to get to the 405th letter.
C A R M E N
1 2 3
The 405th letter in the pattern is the letter R.
4. Check:
How many letters are there in 67 blocks of CARMEN? 67 x 6 = 402
Did I count to the 405th letter? 402 + 3 = 405. Yes
Try solving the following word problem using Polya’s 4-step process.
Word Problem (Primary 1):
Draw the shape that comes next.

Answer: The next shape is ![]()
See the solution here.
These are just a few examples to show you how heuristics are used to solve basic and intermediate word problems in lower primary levels and complex word problems in upper primary levels.
Look out for parts 3, 4 and 5 of this series for the other 9 math heuristics and word problems with step-by-step worked solutions.
This is the second part to S.A.M Math Heuristics series for expert tips on math heuristics.
Read the rest of the “S.A.M Math Heuristics” five-part series below:
Part 1: What Are Heuristics?
Part 3: Math Heuristics: Make A Systematic List, Guess And Check, And Restate The Problem In Another Way
Part 4: Math Heuristics: Solve Part of the Problem, Simplify the Problem and Work Backwards
Part 5: Math Heuristics: Draw a Table, Make Suppositions and Use Before-After Concept
Established in 2010, Seriously Addictive Mathematics (S.A.M) is the world’s largest Singapore Math enrichment program for children aged four to 12. The award-winning S.A.M program is based on the global top-ranking Singapore Math curriculum with a focus on developing problem-solving and thinking skills.
The curriculum is complemented by S.A.M’s two-pillared approach of Classroom Engagement and Worksheet Reinforcement, with an individual learning plan tailored to each child at their own skill level and pace, because no two children learn alike.
This post is brought to you by Seriously Addictive Mathematics.
* * * * *
Like what you see here? Get parenting tips and stories straight to your inbox! Join our mailing list here.
Want to be heard 👂 and seen 👀 by over 100,000 parents in Singapore? We can help! Leave your contact here and we’ll be in touch.





































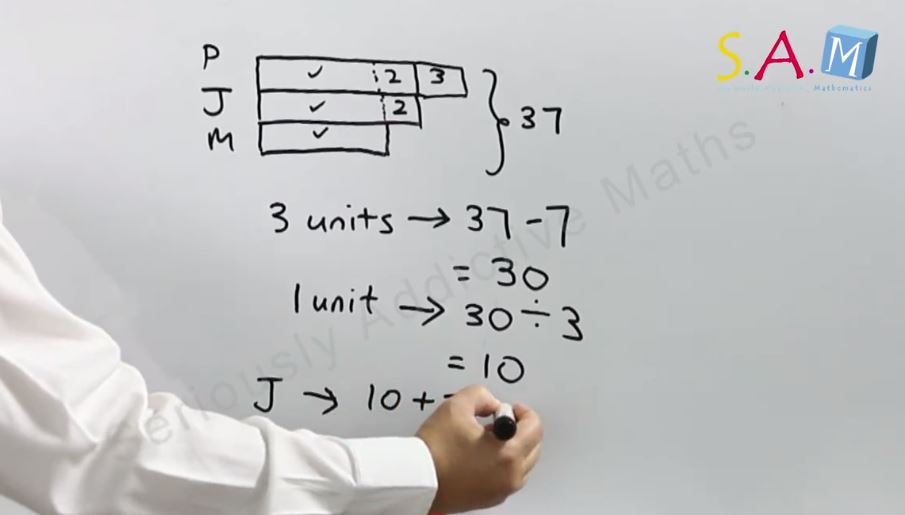















Leave a Comment: